Building Acyclic Directed Graphs (DAGs) using materialized paths with Postgre's ltree.
We are working in a project that has the concept of folders (regular OS directories) but with a twist: the folders in our project can have multiple parents. Said in another way, a folder can be inside two or more folders. Mathematically speaking, they are a tree hierarchy where nodes (folders) have multiple parents. This is called an Acyclic Directed Graph.
How do we map an Acyclic Directed Graph (DAG) in a database?
Although we could use a graph database like Neo4J, we prefer a solution involving SQL Postgres, the backend we are already using for the rest of the application, and benefit from having only to write one query to fetch our data, easier consistency, and not having to learn another technology.
This great post, which I recommend reading, explains how to achieve DAGs with adjacency lists in SQL. We see two drawbacks: 1) not efficient for queries willing to traverse or get the paths, and 2) much custom code to maintain.
Another approach is using Postgres ltree (another recommended lecture), which represents a path of a tree structure. We want this functionality but with multiple parents. In this post we explore how to use multiple paths with ltree to represent DAGs.
Taking the same example as the post I mention above:
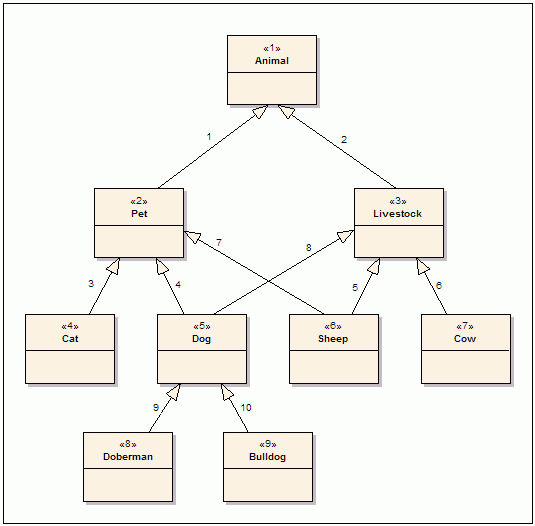
See an explanation of it from here.
First let's define the paths for all animals (nodes):
| nodeId | path (ltree) |
|---|---|
| 1 | 1 |
| 2 | 1.2 |
| 3 | 1.3 |
| 4 | 1.2.4 |
| 5 | 1.2.5 |
| 5 | 1.3.5 |
| 6 | 1.2.6 |
| 6 | 1.3.6 |
| 7 | 1.3.7 |
| 8 | 1.2.5.8 |
| 8 | 1.3.5.8 |
| 9 | 1.2.5.9 |
| 9 | 1.3.5.9 |
We can see how we end up with repeating nodeID, as many as paths we have. For nodes that do not have parent, their path is only themselves (ex. node 1's path is just 1). All nodes have at least one path where they are a leaf.
For given nodes A and B, if we want to denote that B is under A and that both A and B are roots too, we can do it like this: A: A; B: A.B, B.
Following Erdogan's post, if we want to get all livestock (descendants of node 3) we can query all paths that contain node 3. By using ltree this query is as follows:
SELECT *
FROM paths
WHERE path ~ '*.3.*';
If you read ltree documentation, you can be tempted to use <@. Beware that this forces you to write a full path (1.3), thus discarding the other multiple paths. Note that we can avoid listing duplicate nodesId the following way:
SELECT DISTINCT ON (nodeId) *
FROM paths
WHERE path ~ '*.3.*'
From this we can already suppose the design of the table:
CREATE TABLE paths (
nodeId int,
path ltree primary key
);
Note how path is the primary key and nodeID is only there for two reasons: 1. distinct, 2. being a foreign key to a nodes or similar table.
Inserting a node / making a node root
We defined that all nodes have always one path, and by default it is just them (node 1). This is by design. So when inserting a node, ensure you insert a new path. This is the same if you promote a node to be root:
INSERT INTO paths (nodeId, path) VALUES (1, '1');
Insertion of a new edge into the graphs
Erdogan says that "in general, the connection of two vertices with a new edge has to be assumed to be the connection of two discrete graphs. We cannot assume any order of insertion". He then uses Figure 4, the same as below, to illustrate the connection between A and B, when A has some descendants and B some ascendants.
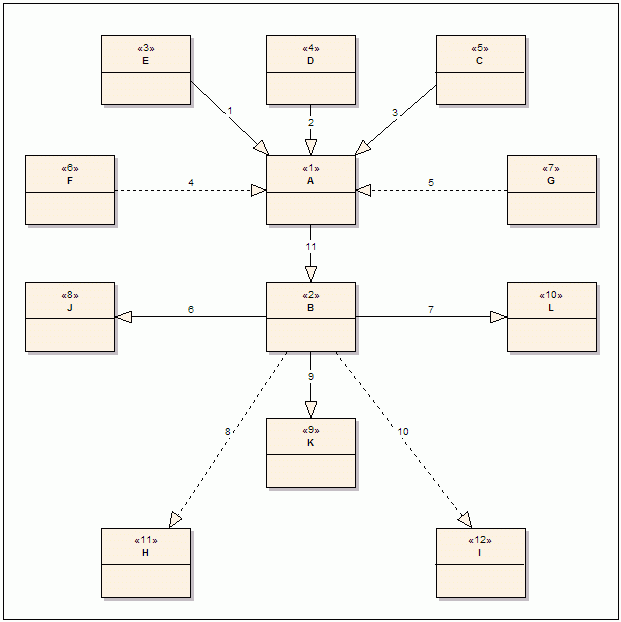
Let's compute the paths of B: J.A, K.B, L.B, H.B, I.B (edges 8 and 10 in the original post are different from the rest, but in here we can assume they are the equal). A has only one path, A itself. When connecting it to B: A copies the paths of B: J.B.A, K.B.A, L.B.A, H.B.A, I.B.A adding itself to the end of each path. So, now A has the paths inherited with B plus the paths that A had originally (A): A, J.B.A, K.B.A, L.B.A, H.B.A, I.B.A.
For a child of A, let's take E for example, this would be as follows: originally E had A.E. And after the connection we have A.E, J.B.A.E, K.B.A.E, L.B.A.E, H.B.A.E, I.B.A.E. Note how A.E has become redundant, as it is included in the other paths. We will deal with this later.
What we are doing all the time is taking the original paths where A is the root and append them to all the paths where B is the leaf. In other words, we are doing the cartesian product between the paths where A is the root and where B is the leaf.
We have done an implementation of this using a psql function. This function is used in our open-source software so there is one difference: our nodes are named lots, and the ids of lots are not int but uuid. Take a look at the function as it is self-documented.
Note that the function performs a final delete. This is to remove the redundant paths that we encountered three paragraphs above (A.E) and the A we end-up with four paragraphs above; it is by design: should A still be a root node when being added under B? In some use-cases would be correct, but not for our personal one.
Deleting paths
For deleting the paths we should perform the inverse operation of the Cartesian product –if that operation existed; we cannot guarantee that reversing the Cartesian product we end-up getting the original graph, so we are forced to try to manually approximate to a satisfying one.
Let's take back the original example:

We want to delete edge 4, deleting the relationship between nodes 5 and 2. The affected paths are the ones from nodes 5, 8, and 9. If the original paths are 5: 1.2.5, 1.3.5; 8: 1.2.5.8, 1.3.5.8; 9: 1.2.5.9, 1.3.5.9, after the deletion they are 5: 1.3.5; 8: 1.3.5.8; 9: 1.3.5.9. Now we face a similar design problem than when creating an edge: should 5 be a root node when deleting edge 4, so 5 ends up with the paths 5, 1.3.5? For our use-case we decided it to be only when 5 has no other parent.
The process is as follows:
- Take all paths that have the subpath
2.5and cut anything above5. So for1.2.5.8, we take1.2out and end up with5.8. - Manage our design decision of 5 not being a root node if it has other parents. So if 5 has multiple paths after applying 1, we delete the path that contains only
5.
If we look at the implementation, we can see an extra step that deletes duplicates. This is because when applying 1 we can end-up with duplicate paths. Take node 8 as an example and assume node 2 has an extra parent called 2', then the paths containing 2.5 are 8: 1.2.5.8, 2'.2.5.8. If we apply step 1, thus removing 1.2 and 2', we end up with 8: 5.8, 5.8 –duplicated redundant paths.
Note too that the method of removing duplicates forces us to have the extra field pathId in our paths table, as by this solution. I am really interested in anyone that can tell me how to delete duplicates without the need of an id.
The table
With everything considered, the final table implementation is:
CREATE TABLE paths (
id uuid primary key default gen_random_uuid(),
nodeId uuid not null references nodes(id),
path ltree not null,
constraint node_path_unique deferrable initially immediate
)
create index path_gist on paths using gist(path);
create index path_btree on paths using btree(path);
- Here I use
uuidinstead ofintto keep it consistent with the insertion / deletion implementations. You can useintor any other if you wish with the respective changes in code; uuids are big ids, specially when taken to strings, which reduces efficiency. - The table
nodesis the table where the node information is. In the implementation of insertion / deletion functions, it is calledlots. - To use
ltreeyou will need to activate it by executing the SQLCREATE EXTENSION ltree;.
Performance
The implementation we follow is slow when performing modifications, specially deleting, but fast when retrieving values. Note that ltree allows indexes that greatly speed-up searches.
todo: get some performance numbers.
Interesting queries
Examples of what you can get with this model. Some queries expect you to substitute X with a node id.
Get root nodes
SELECT nodeId
FROM paths
WHERE nlevel(path) = 1;
Get children of node X
Get only the children of X, not all descendants. A similar query can be done to get the parents.
SELECT nodeId
FROM paths
WHERE path ~ '*.X.*{1}'
Using UUIDs with ltree
Postgre's ltree has a problem: it cannot natively handle UUIDs and neither its string representation, because it can only handle alphanumeric characters, excluding dashes.
We have UUIDs as ids for our nodes. The (inefficient) way we handle them in paths is by storing their string representation changing them from dashes to underscores. You can see in the implementation how we CAST uuids to ltree enabled strings.
Integration with SQLAlchemy
We use SQLAlchemy to represent our models, so you can take a look how we use this with SQLAlchemy.
Conclusion
A materialized paths implementation using Postgres' ltree is not trivial but neither specially difficult, although it still requires custom code to make it work. The big expressivity for ltree allows us to easily analyze and query full paths (ascendants and descendants), or fix to specific hierarchy levels (children, parents).
I rely in the querying of ltree to be efficient, as it is embedded in Postgres and uses indexes. However, more research and testing needs to be done, specially with the usage of GiST indexes.
Finally, this model has yet to pass real-world usage test once we can test this version of the software with users. Both for speed and errors.
I will update this post in the future to answer this concerns. Feedback is always welcomed.
